Par MD
Introduction.
Un récent article avait été consacré à l’analyse d’un graphique très illustratif extrait du « summary for policymakers » (SPM10) du dernier rapport du GIEC dit « AR6 ». Pour éviter les redites, on considérera cet article comme connu des lecteurs. En résumé, le GIEC postule une relation quasi-linéaire entre les émissions anthropiques cumulées de CO2 depuis l’époque « préindustrielle » jusqu’à nos jours et l’évolution des températures. Il en tire une loi de proportionnalité dite TCRE (transient climate response to cumulative CO2 emissions). Il extrapole cette loi pour simuler l’augmentation des températures dans le grand avenir selon plusieurs hypothèses de croissance (les « shared socieconoic pathways » ou SSP).
A titre de rappel, reproduisons à nouveau la figure SPM10 du GIEC.
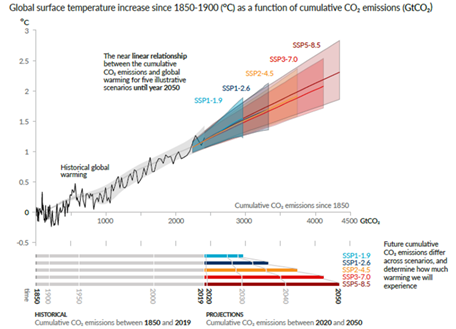
Hypothèse sur la sensibilité climatique : TCR ou TCRE ?
Le concept de sensibilité climatique est à la base de la doctrine traditionnelle du GIEC. A l’échelle décennale ou séculaire, la « transient climate response » (TCR) est définie comme l’augmentation de température censée résulter d’un doublement de la concentration en CO2. Cette théorie a déjà été évoquée sur ce site. Lorsqu’un incrément est proportionnel à un rapport, la relation entre les deux variables est nécessairement logarithmique. Désignons la sensibilité TCR par S (°C), les températures par T (°C) et les concentrations en CO2 par C (ppmv). Les valeurs initiales (dites « préindustrielles », année 1850) sont désignées par T0 et C0. En utilisant le logarithme binaire (lb, de base 2), on aurait ainsi :
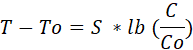
En effet si C/C0 = 2 (doublement) on a bien lb (2) = 1 ; d’où T-T0 (°C) = S * lb (2) ou encore : T-T0 (°C) = S (°C).
Le concept de TCRE (transient climate response to cumulative CO2 emissions)est très différent : il stipule que l’augmentation de température est une fonction linéaire des émissions anthropiques cumulées de CO2 exprimées en masse (milliards de tonnes ou Gt).
Or on peut vérifier, selon le GIEC lui-même, que le rapport C/C0 et les émissions cumulées évoluent parallèlement. Voici pourquoi.
Flux ou le stock de CO2 comme variable explicative ?
Le GIEC fait l’hypothèse fondamentale qu’une partie des émissions anthropiques est absorbée par des « puits » terrestres et océaniques. Il ne subsisterait donc dans l’atmosphère qu’une fraction atmosphérique (« airborne fraction »). Celle-ci est très variable selon les années, mais depuis environ 60 ans elle oscille autour de 44% (±10%) comme l’indique le GIEC (voir AR6, SPM A.1.1). C’est en effet ce que l’on peut constater au vu du graphique ci-dessous.
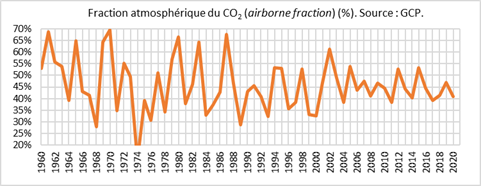
Il en résulte que la masse de CO2 (en Gt) dans l’atmosphère augmente linéairement avec le cumul des émissions anthropiques. Il en va de même de la concentration C (en ppmv) et du rapport C/C0. On le voit sur la courbe ci-dessous, rigoureusement rectiligne pour les soixante dernières années (les variations annuelles sont atténuées du fait qu’il s’agit de cumuls).
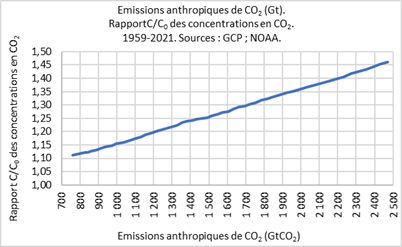
Lecture : en 1959, les émissions anthropiques cumulées depuis 1850 étaient de 747 GtCO2. En 2019, de 2 411 Gt, soit 1 694 Gt de plus ; la concentration était passée de 316 à 412 (ppmv) soit 96 ppmv de plus ; et le rapport C/C0 de 1,11 à 1,44.
Par conséquent, on peut indifféremment choisir comme variable « explicative » soit le cumul des émissions anthropiques de CO2 (Gt) comme le fait le GIEC, soit le stock de CO2 dans l’atmosphère (Gt), soit la concentration C de CO2 (ppmv), soit enfin le rapport C/C0 (concentration relativement à une valeur initiale).
Les mesures directes de la concentration en CO2 ont commencé en 1959
Dans ce qui suit, on se limitera à la période d’une soixantaine d’années pendant laquelle la fraction atmosphérique est réputée constante par le GIEC, soit depuis 1959, qui sera donc choisie comme nouvelle date de référence initiale. Il se trouve que cette date est aussi celle qui correspond au début des mesures directes de concentration en CO2 à l’observatoire NOAA de Mauna Loa. Ces mesures sont reconnues au niveau international et sont probablement les plus fiables. On rajoutera les données pour 2020 et 2021, qui ne figuraient pas dans le rapport du GIEC.
Évolution des températures depuis 1959
Reprenons, en le limitant dans le temps, un graphique analogue à celui de l’article précédent. On a superposé les deux échelles (cumul des émissions anthropiques et rapport C/C0). Les compteurs sont remis à zéro en 1959 (cumul = 0, C=C0 et C/C0=1). Notons que la température Hadcrut5 de 1959 prise cette fois comme origine est de 0,3°C au-dessus de celle de la « période préindustrielle » 1850-1900.
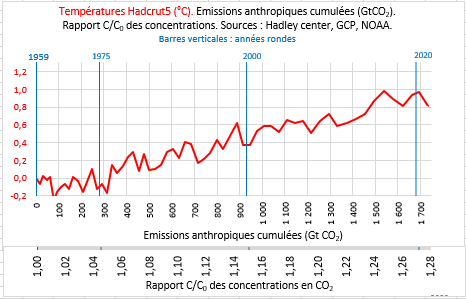
Évolution des températures de 1959 à 2021 : tendance linéaire ou logarithmique ?
On peut compléter le graphique précédent en lui superposant le modèle linéaire TCRE du GIEC (soit +0,45°C pour 1 000 GtCO2) représenté par la droite verte.
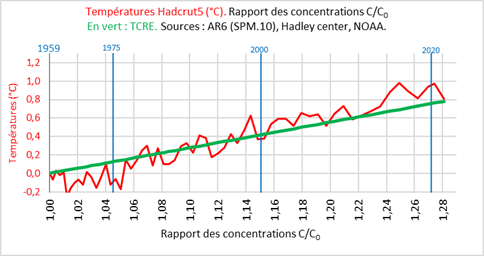
On voit que le modèle simule tant bien que mal l’évolution des températures de 1959 à 2021.
Mais on pourrait faire une autre simulation, en adoptant cette fois une fonction logarithmique, et en essayant par tâtonnement de la rapprocher de la fonction linéaire. On trouve que la valeur adéquate de sensibilité (TCR) serait S = 2,2°C (cette valeur se situe à l’intérieur de la fourchette traditionnellement retenue). La fonction s’écrirait donc : T-T0 = 2,2 * lb (C/C0), représentée par la courbe violette surajoutée au graphique précédent.
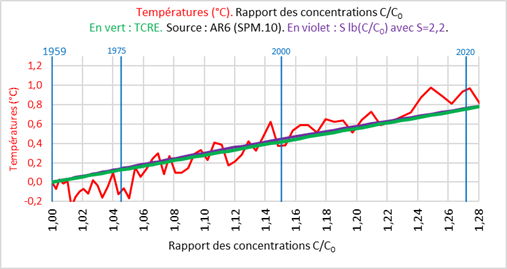
Sur la période considérée, les deux simulations sont pratiquement confondues. Au-delà, les courbes commenceraient à diverger lentement, comme on le voit ci-dessous dans l’exemple du scénario médian SSP2-4.5, la fraction atmosphérique étant supposée se maintenir à 44%. Ce n’est qu’une simple illustration sur laquelle on ne s’appesantira pas.
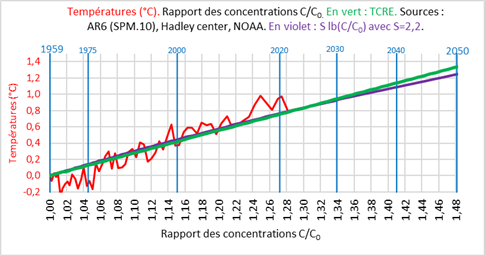
La différence est certes modeste et reste dans les fourchettes d’incertitudes. Mais on sait que la science officielle scrute le moindre dixième de degré en plus ou en moins et en tire bruyamment toutes sortes de conséquences.
Conclusion.
Précisons que le présent exercice doit être considéré comme une simple distraction mathématique. Il ne s’agit pas de substituer un « modèle » au « modèle » officiel. D’ailleurs rien n’interdirait de tester d’autres fonctions algébriques de degrés variés qui pourraient tout aussi bien (ou aussi mal) « coller » avec les observations de la période 1959-2021.
Les deux fonctions envisagées ici, que l’on sache, ne reposent aucunement sur des lois physiques indiscutables ; ce ne sont que des formules empiriques voire purement visuelles plaquées sur des données factuelles. Les extrapoler à des horizons éloignés n’en est que plus hasardeux.

Attention, sur les 3 derniers graphiques, le tracé des simulations linéaires et logarithmique est trompeur. Il joint la valeur initiale ( à C/C0 1,00) de la température à sa valeur finale ( à C/C0 1,28). De ce fait, les tracés ne sont représentatifs que des points extrêmes et non de l’ensemble des points
Des régressions linéaires et logarithmiques sur l’ensemble des points auraient montré que les deux corrélations (et non simulations) sont bonnes.
Par ailleurs, on peut douter que les scientifiques (et non le GIEC qui n’est qu’un éditeur) aient choisi une corrélation alors qu’ils savent calculer l’évolution de la température en fonction des tous les GES et qu’ils fixent l’évolution du détail de ceux ci dans les scénarios du futur.
JeanRen
Vous avez tout à fait raison : les deux « courbes » du graphique joignent pratiquement les deux points extrêmes (1959 et 2021) de la température Hadcrut5. Voici comment.
Comme vous le remarquez à juste titre, la fonction dessinée en vert n’est pas une régression linéaire : elle n’est autre que celle retenue par le GIEC, à savoir 0,45°C pour 1 000 GtCO2 anthropiques émises. Entre 1959 et 2021, les émissions se sont élevées à environ 1 750 Gt. La fonction donne donc une augmentation de température de 1,750 x 0,45 # 0,79°C, à comparer avec l’augmentation de température Hadcrut5 qui a été de 0,81°C. Sur cette période précise, la fonction prédictive du GIEC aura donc été presque adéquate. L’avenir dira s’il ne s’agit que d’un pur hasard. La fonction logarithmique en violet n’est là qu’à titre de provocation.
Sur votre second point, il n’est pas douteux que le GIEC a bien défini une corrélation, exprimée sans ambiguïté comme vous pouvez le vérifier en consultant le SPM de l’AR6 (figure SPM10 et §D.1.1). Voir aussi mon article précédent (plus sérieux celui-là) sur le même sujet.
Merci en tous cas pour votre lecture attentive.
MD