Le rapport AR6 et le niveau de la mer, 3ème partie : proposition d’une méthode de prévision statistiquement valide

Andy May

Le texte qui suit est la traduction du troisième article publié par Andy May sur le site Watt’s Up With That. Pour accéder à la traduction des deux premiers articles de la série en cliquer ici (1ère partie) ou là (2ème partie).

Dans la première de cette série, nous avons examiné les données et arguments exposés dans le rapport AR6 du GIEC étayer leur conclusion selon laquelle l’élévation du niveau de la mer s’accélère. Dans la deuxième partie, nous avons examiné en profondeur les données d’observation de l’élévation du niveau de la mer au cours des 120 dernières années et des composantes modélisées de cette élévation. Nous en avons conclu dans la première partie que les preuves statistiques présentées dans le rapport AR6 pour expliquer l’accélération de l’élévation du niveau de la mer étaient brutes et choisies “à dessein”. Dans deuxième partie nous avons vu que l’erreur sur les estimations de l’élévation du niveau de la mer et aussi sur l’estimation des composantes de cette élévation est très importante. Le niveau d’erreur nous a empêché de déterminer avec certitude l’accélération, mais les données ont révélé une oscillation d’environ 60 ans qui correspond aux cycles océaniques naturels connus.

Les outils statistiques modernes nous permettent de prévoir les séries chronologiques, comme le changement du GMSL (niveau moyen mondial de la mer), d’une manière plus valide et sophistiquée que de simplement comparer des ajustements par la méthode des moindres carrés appliquées à des données “sélectionnés” comme le fait le GIEC dans AR6. Nos prévisions sont basées sur des statistiques pures. C’est la bonne méthode mais les résultats ne sont pas nécessairement corrects, c’est le problème avec les statistiques.

La figure 1 est un graphique construit avec les données sur le niveau de la mer de la NOAA. En l’examinant de plus près on peut voir qu’il est auto corrélé , ce qui signifie que l’estimation du niveau moyen de la mer de chaque trimestre dépend fortement des valeurs du trimestre précédent. Bien que l’’autocorrélation soit importante à prendre en compte dans la régression des moindres carrés, elle est systématiquement ignorée par le GIEC.

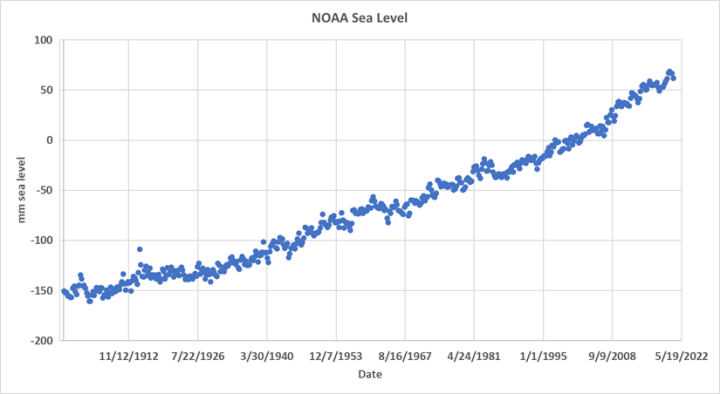
 La figure 2 trace chaque estimation du niveau de la mer par rapport à l’estimation précédente, c’est ce qu’on appelle un tracé du premier décalage et la corrélation des deux est une mesure d’autocorrélation. Le R 2 du premier décalage est de 0,97, donc le niveau de la mer est très autocorrélé. Ceci est évident mais signifie que les statistiques d’ajustement linéaire des moindres carrés normaux ne sont pas valides, les statistiques des moindres carrés, telles que R 2 , supposent que les erreurs de régression sont indépendantes. Les moindres carrés, tels qu’utilisés dans le rapport AR6 pour montrer l’accélération, sont inappropriés avec un ensemble de données comme celui-ci. La plupart de toute valeur donnée dépend fortement de la valeur précédente. Cela signifie que l’erreur quadratique moyenne (MSE) sera beaucoup trop petite, ce qui rendra l’erreur d’ajustement trop petite. En conséquence, toute ligne des moindres carrés des données de la figure 1 ou toute partie de ces données est statistiquement inutile, à moins que l’autocorrélation ne soit prise en compte.

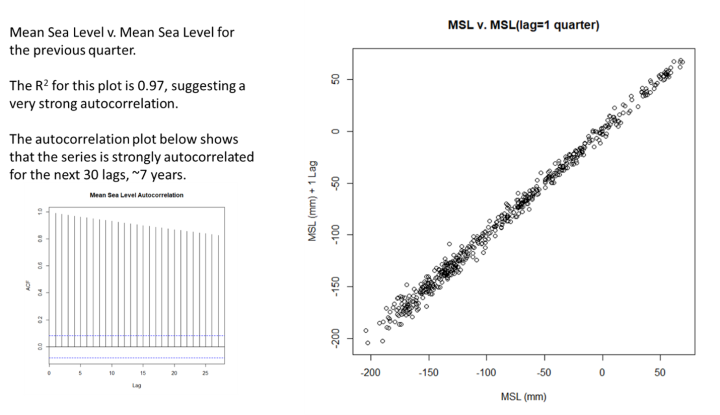
Alors, comment pouvons-nous prévoir la GMSL de manière statistiquement valide ? Nous ne pouvons clairement pas utiliser les moindres carrés et devons appliquer des techniques plus avancées. La première étape consiste à supprimer l’autocorrélation des données, cela se fait normalement en soustrayant la valeur GMSL précédente de la valeur actuelle et en progressant de cette manière dans l’ensemble de données. Cela donne le graphique de la figure 3.

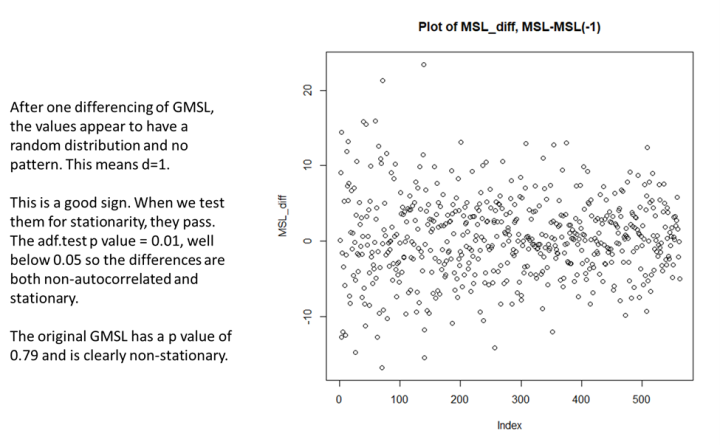
Les premières données de différence de GMSL semblent assez bonnes, très proches d’un bruit blanc. C’est exactement ce que nous voulons pour une analyse et une prévision statistiques valides. Nous allons utiliser une fonction R appelée “Arima” (*) pour créer notre prévision de GMSL, et cette fonction nécessite trois paramètres pour fonctionner p, d et q. Ces paramètres indiquent à Arima comment conditionner les données d’entrée et construire un modèle capable de projeter des valeurs futures valides. Le graphique de la figure 3 nous montre que “d” est égal à un. Cela signifie que prendre une différence de valeurs adjacentes supprime l’autocorrélation. Il faut aussi que les données soient stationnaires, c’est-à-dire que les propriétés statistiques ne changent pas avec le temps (de gauche à droite). L’ensemble de données d’origine (Figure 1) n’était clairement pas stationnaire, et cela n’a pas d’importance car nous ne voulons tout simplement pas que la façon dont le GMSL change soit une fonction du temps pour cette analyse. Le Test augmenté de Dickey-Fuller ou test ADF  confirme cela, car l’ensemble de données d’origine a une valeur ADF p de 0,79, ce qui signifie qu’il n’est pas stationnaire. La valeur Arima p n’est pas la même que le test p statistique.

Les différences tracées dans la figure 3 ont une valeur ADF p de 0,01, bien inférieure à 0,05, le seuil nécessaire pour montrer la stationnarité. Les données sont stationnaires lorsque la distribution sur la période étudiée est uniformément répartie autour de la moyenne. C’est-à-dire que la distribution, vers le haut et vers le bas, ne varie pas de manière significative avec l’axe du temps (x).

Ensuite, nous devons dériver les valeurs Arima p et q. Pour cela, nous avons besoin des tracés ACF (autocorrélation) et PACF (autocorrélation partielle) illustrés à la figure 4.

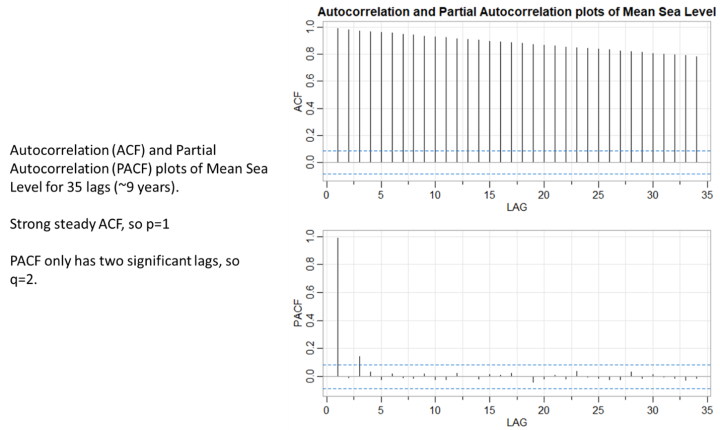
L’analyse de la série temporelle du GMSL nous donne un ensemble de paramètres Arima de (1,1,2) pour (p,d,q). Nous pouvons également exécuter une fonction R appelée auto.arima pour voir quels paramètres elle recommande. Nous constatons qu’il s’installe également sur (1,1,2). C’est une bonne confirmation que notre sélection de paramètres est correcte. La figure 5 trace les résultats.

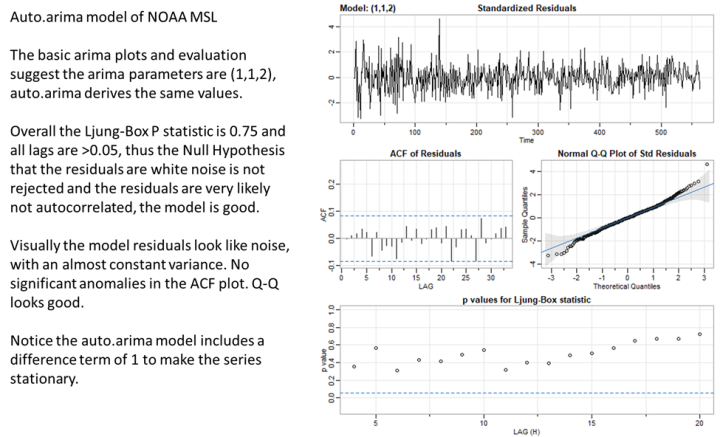
La figure 5 nous indique que le modèle capture avec succès l’essence des tendances du niveau moyen de la mer de 1880 à 2020. Les résidus du modèle ne montrent aucune tendance et ils ne sont pas autocorrélés. La figure 6 montre la prévision arima du modèle (1,1,2).

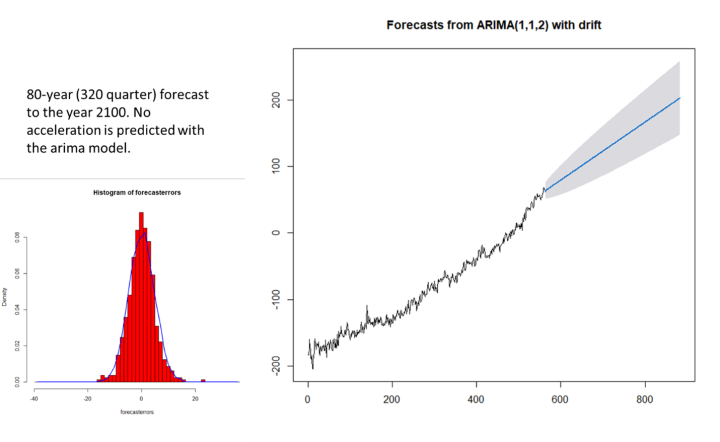
La figure 7 est un graphique de la prévision tracé par Excel qui est plus facile à lire. Les prévisions que nous avons créées prédisent que la GMSL augmentera entre 148 mm (6 pouces) et 258 mm (10 pouces) d’ici 2100. De nombreux chercheurs qualifient cela d’ alarmant, mais les humains se sont adaptés avec succès à des taux d’élévation du niveau de la mer beaucoup plus élevés dans le passé, comme nous le pouvons voir dans la figure 2 de la 1ère partie de cet article , et ils l’ont fait sans les moyens technologiques dont nous disposons aujourd’hui. Au 20e siècle, le niveau de la mer a augmenté de 139 mm. Quelqu’un l’a-t-il remarqué ou s’en est-t-il soucié, à part quelques chercheurs ?

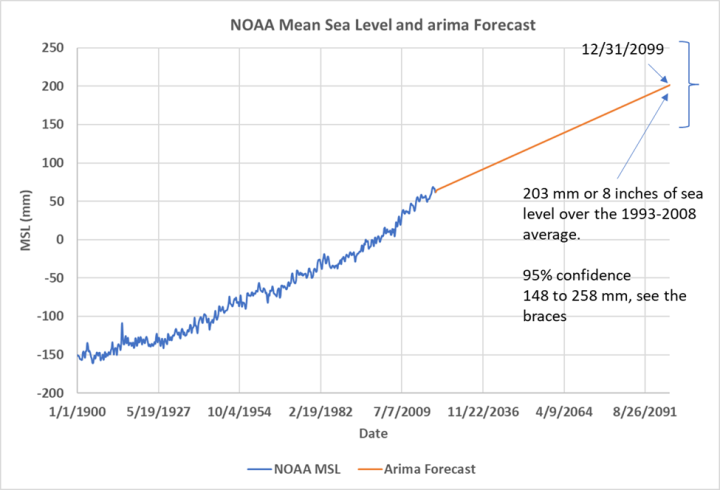
Conclusions

Aux États-Unis, nous appellerions la tentative du rapport ‘AR6 de nous convaincre que le taux d’augmentation de la GMSL s’accélère, en utilisant des courbes issues de la méthode des moindres carrés appliquée à des valeurs adjacentes sélectionnées “à dessein” comme scolaire ou non sophistiquée. Leur méthode est problématique car le GMSL est fortement autocorrélée et non stationnaire, ce qui rend invalides leurs ajustements par les moindres carrés sélectionnés et leurs statistiques des moindres carrés.

Notre ajustement, utilisant la fonction R Arima, est au moins statistiquement valide. Nous avons spécifiquement corrigé l’autocorrélation et forcé la série à être stationnaire. Nous avons également abordé l’autocorrélation partielle mineure laissée à un quart et trois quarts. Les résidus de notre modèle ont réussi à la fois le test global de Ljung-Box et les tests de Ljung-Box à décalage multiple pour le bruit blanc, ce qui signifie que le modèle Arima a correctement capturé la tendance sur 140 ans dans les données sur le niveau de la mer de la NOAA.

Ainsi, alors que le rapport AR6 a sélectionné des périodes pour étayer sa conclusion selon laquelle la GMSL s’accélère, nous sommes parvenus à la conclusion opposée en utilisant toutes les données d’une manière statistiquement valide. Cela ne signifie pas que nos prévisions sont correctes, mais cela signifie que les spéculations du rapport ’AR6 selon lesquelles le niveau de la mer pourrait monter de 5 mètres d’ici 2150 est extrêmement improbable et peut être qualifiée de spéculation irresponsable. Notre analyse n’a trouvé aucune preuve statistique d’accélération et a produit une extrapolation linéaire.

Alors que le réchauffement de la surface de la Terre est clairement la raison pour laquelle les glaciers terrestres fondent, ce qui contribue à l’élévation du niveau de la mer, le rapport AR6 ne fournit aucune preuve que le réchauffement est causé par les activités humaines. Ils utilisent des modèles pour déduire que les humains en sont la cause, mais malheureusement, ces modèles ne sont pas non plus statistiquement valides, comme indiqué dans la 2ème partie de cet article , dans cet autre article , et par McKitrick et Christy (McKitrick & Christy, 2018). Nous sommes tous d’accord pour dire que les humains ont probablement un certain impact sur le réchauffement atmosphérique, mais nous ne savons pas faire la part entre les activités humaines et les causes naturelles, car nous sortons d’un petit âge glaciaire inhabituellement froid pendant la période “préindustrielle”. De plus, comme nous l’avons vu dans la 2ème partie de cet article, les taux d’élévation du niveau de la mer sur 30 ans révèlent une oscillation d’origine clairement naturelle. La fonte des glaciers et des calottes glaciaires sont probablement responsables de la majeure partie de l’élévation du niveau de la mer, comme l’indique le rapport AR6, mais la fraction humaine de ce réchauffement pourrait être assez faible.

Ainsi, d’un point de vue purement statistique, les assertions du rapport nous paraissent invalides. Une analyse correcte des données conduit à une prévision d’environ 20 cm d’élévation du niveau de la mer d’ici 2100.

Les données et le code R pour créer les figures de ce chapitre peuvent être téléchargés ici . Le code R et la feuille de calcul fournissent beaucoup plus de détails sur les prévisions arima, y ​​compris les références non fournies ci-dessous.

Ouvrages cités

McKitrick, R., & Christy, J. (2018, 6 juillet). Un test du taux de réchauffement tropical de 200 à 300 hPa dans les modèles climatiques, Earth and Space Science. Sciences de la Terre et de l’espace, 5 (9), 529-536. Extrait de https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2018EA000401